Usage of the CLUSTER.INP file

The description of the keywords is listed. If none of the options is specified in the input file, the underlined one is used by default. The boldface printed part (first five letters) of the keywords and options are mandatory for the correct input interpretation by NRLMOL. Therefore, OPTIMIZATION, OPTIMIZE, and OPTIM are all allowed input forms for the keyword OPTIMIZATION.

Keyword GEOMETRY

This keyword is mandatory! It specifies the molecular geometry. Options:

CARTESIAN / ZMATRIX

CARTESIAN

The molecular structure is given in Cartesian coordinates.

ZMATRIX

The molecular structure is defined by a Z-matrix. The form Z-MATRIX is equivalent to ZMATRIX. ANGSTROM / BOHR

ANGSTROM

Coordinates or bond distances are given in Ångströms.

BOHR

Coordinates or bond distances are given in atomic units. Description: The geometry is read in the keyword body of GEOMETRY in free format, one line for each atom. In the case of a CARTESIAN input the atomic symbol (e.g. H), which may carry an identification number (e.g. H1), and the x, y and z coordinates of each atom of the system must be specified. As an example, the geometry of H2O may be specified as:

GEOMETRY CARTESIAN ANGSTROM

O 0.00 0.00 0.00

H 0.76 0.00 0.52

H -0.76 0.00 0.52

The Cartesian coordinates of an individual atom, defined by the atomic symbol (e.g. H2), or an atom group, defined by the element symbol (e.g. H), can be frozen during the geometry optimization in redundant coordinates. To keep all three degrees of freedom of an atom fixed the corresponding atomic symbol or element symbol has to be specified with the string XYZ in the keyword body of CONSTANTS. The string X will freeze only the x coordinate of the corresponding atom, the string XY fixes the x and y coordinates, etc. In the following example, the oxygen atom is kept frozen and the movements of all hydrogen atoms are restricted to the xz-plane (y coordinate frozen) during the optimization.

GEOMETRY CARTESIAN ANGSTROM

O 0.00 0.00 0.00

H 0.76 0.00 0.52

H -0.76 0.00 0.52

#

CONSTANTS

O XYZ

H Y

The comment line (#) is given only for clarity. The following input for a water-like system consists of a frozen oxygen atom, a hydrogen atom, H1, fixed in the xz-plane.

GEOMETRY CARTESIAN ANGSTROM

O 0.00 0.00 0.00

H1 0.76 0.00 0.52

H2 -0.76 0.00 0.52

#

CONSTANTS

O XYZ

H1 Y

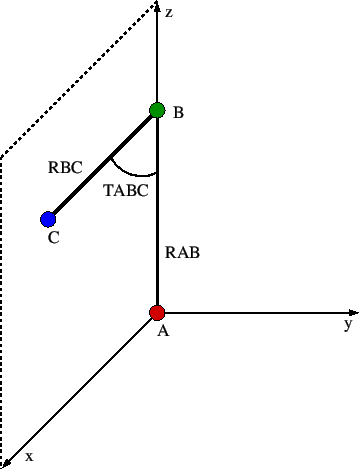
If the geometry of the system is given by a Z-matrix, using the option ZMATRIX, each line in the keyword body of GEOMETRY describes the connectivity of the atom, which again is defined by its atomic symbol. The first atom of the Z-matrix defines the origin of the input (see Figure 1) and therefore has no connectivity information.

Figure 1: Orientation of the first three atoms defined in the Z-matrix.

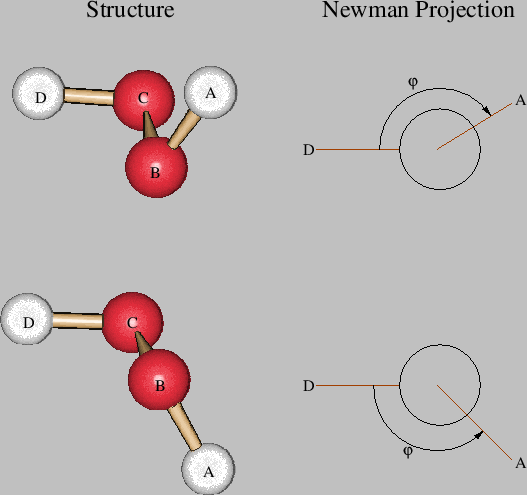
The second atom lies on the z-axis of the input coordinate system and is connected to the first atom at a distance RAB. The third atom lies in the xz-plane and connects to the two previously defined atoms at a distance RBC and an angle TABC. Each of the following atoms is defined by an input line in free format containing the information: LABEL NB RAB NC TABC ND PABCD Here LABEL is the atomic label of atom A. NB, NC, and ND are the Z-matrix line numbers or the atomic labels of the atoms B, C and D which respect to which atom A is defined by a length (RAB), angle (TABC), and dihedral angle (PABCD). These are the so-called internal coordinates of the system. Their values are given by RAB (in Ångström or Bohr), TABC, and PABCD (in degrees), respectively. The maximum length of these numbers in the Z-matrix is limited to ten characters. The dihedral angle is defined by the angle between the planes spanned by the atoms {A, B, C} and {B, C, D}, respectively. The sign of the dihedral angle is defined according to the Newman projection shown in Figure 2. If the projection angle is oriented clockwise then the dihedral angle is positive.

Figure 2: Definition of positive (top) and negative (bottom) dihedral angles in deMon.

Instead of giving the values for RAB, TABC, and PABCD directly in the Z-matrix, they may also be represented by symbolic strings with no more than eight characters each. These strings must be assigned to CONSTANT or VARIABLE values (see corresponding KEYWORDS) in the input, as the following example

GEOMETRY ZMATRIX ANGSTROM

C1

C2 C1 rCC

H1 C1 rCH C2 aCCH

H2 C1 rCH C2 aCCH H1 dHCCH

H3 C2 rCH C1 aCCH H2 dHCCH

H4 C2 rCH C1 aCCH H1 dHCCH

#

VARIABLES

rCC 1.3390

rCH 1.0850

aCCH 121.09

#

CONSTANT

dHCCH 180.0

The internal coordinates listed under VARIABLES are changed during geometry optimization, whereas the coordinates listed under CONSTANTS are kept frozen. The RAB, TABC, and PABCD values that are directly defined in the Z-matrix always are interpreted as constants. If one uses internal coordinates, dummy atoms often are useful. The atomic symbol X has been reserved for them. The following example shows the use of a dummy atom in the definition of HCN.

GEOMETRY ZMATRIX ANGSTROM

H

C 1 R1

X 2 1.0 1 90.0

N 2 R2 3 A1 1 180.0

#

VARIABLES

R1 1.089

R3 1.166

A1 90.00

Here the dummy atom is used to avoid a 180o angle which might cause problems in a geometry optimization. Please note that the structure parameters which are defined inside the Z-matrix are kept constant during structure optimization.

Keyword CONSTANTS

This keyword assigns constant Cartesian and internal structure parameters. Options: None

Description:

The body of CONSTANTS lists all atoms and internal coordinates which are kept frozen during the geometry optimization. The atomic or element symbol with the string XYZ is used to freeze the atom or group of atoms in redundant coordinates. The string X will only freeze the x coordinate of the atom, the string XY the x and y coordinates, etc. For internal coordinate inputs, freezing of a particular degree of freedom is done by giving the symbolic coordinate string of the Z-matrix and its assigned (frozen) value (real number). The maximum length of the value string is 15 characters. Please note that structure parameters that are explicitly defined inside the Z-matrix always are treated as CONSTANTS in optimizations.

Constants

H XYZ

A 120.0

Keyword VARIABLES

This keyword assigns variable internal coordinates.

Options: None

Description:

The body of VARIABLES collects all symbolic coordinate strings of the Z-matrix, along with their initial values, which are to be optimized. The maximum length for the variable value assigned under VARIABLES is 15 characters. The maximum length for symbolic strings in the Z-matrix that denote variables or constants is 8 characters.

Keyword NETSPIN

This keyword specifies the netspin of the system, i.e. number of unpaired electrons. Options: FIXED

<Real>

Netspin

FIXED

The netspin is fixed and not optimized automatically.

Description:

The default netspin are 0 for closed and 1 for open shell systems. The program will check automatically if the specified multiplicity is allowed for the given molecular system and its charge.

Keyword CHARGE

This keyword specifies the net charge of the system.

Options:

<Real>

Charge of the system.

Description:

The default net charge is 0. Beware that net negative charges (anions) can lead to unphysical behavior with simple approximate density functionals.[1]

Keyword OPTIMIZATION

This keyword controls the local geometry optimization. Options:

REDUNDANT / CARTESIAN

REDUNDANT

The optimization is performed in delocalized redundant internal coordinates. This is the default.

CARTESIAN

The optimization is performed in Cartesian coordinates.

TOL=<Real>

Optimization convergence criterion for MAX gradient. Default is 1 x 10-3 atomic units.

STEP=<Real>

Maximum step size in optimization. Default is 0.3 atomic units.

Description:

By default, deMon2k uses delocalized internal redundant coordinates for the geometry optimization or transition state search [2,3]. For full geometry optimizations, this is also the recommended method. Because of the possible linear dependencies of the internal coordinates defined in the Z-matrix, optimization in these coordinates may become problematic for larger systems (> 30 atoms). With the REDUNDANT option and a Cartesian input, NRLMOL constructs a Z-matrix from the Cartesian input and a set of linear combinations of internal coordinates (delocalized coordinates) which avoids linear dependencies. This option should be used if an optimization gets stuck and has to be restarted. With the REDUNDANT option and an internal Z-matrix input, the optimization also is performed in delocalized internal redundant coordinates. However, now the user-defined internal coordinates of the Z-matrix are included in the delocalized internal redundant coordinates. At each optimization step these delocalized internal redundant coordinates are transformed back to the coordinates of the Z-matrix input. Table 1 shows the relationships between the types of input and types of optimization options. Each cell in that Table contains two values. The upper value shows the coordinate system used for an optimization step, while the lower value shows the coordinate system.

Table 1: Relationship between different options for the keywords GEOMETRY and OPTIMIZATION.

With the TOL option the optimization convergence criterion can be specified. Convergence of the optimization is based on the remaining maximum forces. The TOL option specifies the maximum force convergence criterion. The maximum step length (in atomic units) used in the optimization can be specified with the STEP option. The (P)-RFO steps [4,5] can be chosen by selecting the RFO STEPTYPE (see KEYWORD). Both methods guarantee that the (right) Hessian structure (no negative eigenvalues) is preserved.

Keyword HESSIAN

This keyword specifies the choice of the starting Hessian for geometry optimization or transition state search. Options: BAKER / FISHER / UNITY / INTERNAL / LINDH / RESTART

BAKER

Starting Hessian constructed from Baker force weights. This is the default for the internal optimization.

FISHER

Starting Hessian constructed from Fisher force weights. This is the default for the redundant optimization.

UNITY

The unit matrix is used as starting Hessian. This is the default for the Cartesian optimization.

INTERNAL

Starting Hessian from the unit matrix of an internal Hessian constructed from an auxiliary Z-Matrix.

LINDH

Starting Hessian constructed from Lindh force weights.

RESTART

Starting Hessian is read from the restart file xxxxx.

Description:

With the options BAKER, FISHER, and LINDH, a starting Hessian in primitive redundant coordinates is generated, then transformed into the coordinate system used for the optimization. For the BAKER option, the diagonal elements for the primitive bonds, bends, and dihedral angles are set to 0.5, 0.2 and 0.1, respectively [2]. For the FISHER option, the diagonal elements are calculated according to the empirical rules of Fisher et al. [7]. This is the default for the starting Hessian of the default redundant optimization. With the option LINDH, the diagonal elements are calculated according to the empirical rules of Lindh et al. [8]. For a Cartesian optimization, a unit Cartesian starting Hessian is the default option. If other options are chosen for Cartesian optimizations, an auxiliary Z-Matrix is constructed from the Cartesian input, and either a unit (option INTERNAL) or an empirical (options BAKER, FISHER, or LINDH) internal Hessian matrix (options BAKER, FISHER, or LINDH) is calculated. Then, this internal Hessian is transformed into the Cartesian starting Hessian.

A unit matrix starting Hessian in the space of the primitive redundant coordinates (for redundant optimizations), in the space of the internal Z-matrix coordinates (for internal optimizations), or in the space of the Cartesian coordinates is specified with the option UNITY. With the optios RESTART the starting Hessian is read from the restart file. The (updated) Hessian matrix is written to the restart file at the end of each optimization step. With the RESTART option, that Hessian can be recovered.

Keyword UPDATE

This keyword controls the Hessian update method during geometry optimization.

Options:

BFGS / POWELL / BERNY / DFP / MSP / SR1

BFGS

Broyden, Fletcher, Goldfarb, Shanno (BFGS) update [9-12]. This is the default for the geometry optimization.

POWELL

Powell update [6].

BERNY

Berny update from H.B. Schlegel [13].

DFP

Davidon, Fletcher, Powell update [14-15].

MSP

Murtagh-Sargent-Powell update [16].

SR1

Symmetric rank-one update [17].

Description:

For the optimization in redundant coordinates, the BFGS update is recommended. For optimization in internal coordinates, the BERNY update may be preferred.

Keyword STEPTYPE

With this keyword the geometry optimization step is selected.

Options:

LEVENBERG / RFO / WALK / DESCENT

RFO

Rational function optimization.

WALK

Potential energy surface walking.

DESCENT

Steepest descent.

LEVENBERG

Levenberg-Marquardt.

Description:

By default NRLMOL uses Levenberg-Marquardt steps [18,19] with robust root finding [20] in the structure optimization by the uphill trust region method [16,21]. Alternatively, RFO [22] and WALK [23] steps are available for restricted step method minimizations [24].

Keyword POPULATION

This keyword selects a population analysis. Options: NBO

NBO

Create input file for an NBO analysis.

Description:

NRLMOL generates the input file for the NBO orbital-based population analysis for use with the NBO program [25].

Keyword VISUALIZATION

This keyword activates the interface to the visualization programs JMOL [26], MOLDEN [27] and MOLEKEL [28]. Options: JMOL / MOLDEN EGMIN=0.5 EGMAX=0.5

JMOL

The JMOL interface is activated. The JMOL input is written to the CLUSTER.mol file. This is the default.

MOLDEN

The MOLDEN interface is activated. The MOLDEN input is written to the CLUSTER.mol file. This is also a valid input file for MOLEKEL. FULL / OPT

FULL

A full JMOL or MOLDEN input is written. This is the default if the option JMOL is set.

OPT

The molecular structures as well as the forces and step sizes of each optimization step are written to the CLUSTER.mol file. This option is only valid for the MOLDEN interface.

EGMIN

Minimum gap for printing MO orbitals. Default = 0.5 hartrees Orbitals within the EFERMIN – EGMIN range of energies will be written into the JMOL or MOLDEN files.

EGMAX

Maxium gap for printing MO orbitals. Default = 0.5 hartrees Orbitals within the EFERMIN + EGMAX range of energies will be written into the JMOL or MOLDEN files

Description: The options JMOL and MOLDEN are mutually exclusive. They activate the writing of the interface file CLUSTER.mol. With the options FULL and OPT the output data are selected. Note that for large systems, the FULL option of the VISUALIZATION keyword produces very large interface files.

Keyword PRINT

Optional printing can be activated with this keyword. Options:

OPT

Generate full optimization output.

PRI

Print primitive internal coordinates.

MOS

Print molecular orbital energies, occupations and coefficients.

PMAT

Print density matrix.

SMAT

Print overlap matrix.

Description:

All matrices that are changing during the SCF (e.g. PMAT, MOS, etc.) can be printed for each cycle. The following example activates the printing of the density matrix: PRINT PMAT

In general, several print options will produce large outputs. By default only the MO’s within the ranges defined by the EGMIN=0.5 EGMAX=0.5 will be printed. These thresholds may be changed via the VISUALIZATION keyword.

References

1. 14. Rösch, S.B. Trickey, J. Chem. Phys. 106, 8940 (1997).
2. 10. Baker, A. Kessi, B. Delley, J. Chem. Phys. 105, 192 (1996).
3. J.U. Reveles, Geometry Optimization in LCGTO-DFT Methods with Auxiliary Functions, Ph.D. Thesis, Cinvestav, Mexico-City (2004).
4. 1. Banerjee, N. Adams, J. Simons, R. Shepard, J. Phys. Chem. 89, 52 (1985).
5. 10. Baker, J. Comput. Chem. 7, 385 (1986).
6. M.J.D. Powell, Math. Prog. 1, 26 (1971).
7. T.H. Fisher, J. Almlöf, J. Phys. Chem. 96, 9768 (1992).
8. 18. Lindh, A. Bernhardsson, G. Karlström, P. Malmqvist, Chem. Phys. Lett. 241, 423 (1995).
9. C.G. Broyden, J. Inst. Maths. Applns. 6, 76 (1970); ibid. 6, 222 (1970).
10. 18. Fletcher, Computer J. 13, 317 (1970).
11. 4. Goldfarb, Maths. Comp. 24, 23 (1970).
12. D.F. Shanno, Maths. Comp. 24, 647 (1970).
13. H.B. Schlegel, J. Comput. Chem. 3, 214 (1982).
14. W.C. Davidon, AEC Res. & Dev. Report ANL-5990 (1959).
15. 18. Fletcher, M.J.D. Powell, Computer J. 6, 163 (1963).
16. J.M. Bofill, J. Comput. Chem. 15, 1 (1994).
17. 10. Nocedal, S.J. Wright, Numerical Optimization (Springer, New York, 1999).
18. 11. Levenberg, Quart. Appl. Math. 2, 164 (1944).
19. D.W. Marquardt, SIAM J. 11, 431 (1963).
20. J.M. del Campo, A.M. Köster, Croatica Chemica Acta 82, A029 (2009).
21. 16. Culot, G. Dive, V.H. Nguyen, J.M. Ghuysen, Theor. Chim. Acta 82, 189 (1992).
22. 1. Banerjee, N. Adams, J. Simons, R. Shepard, J. Phys. Chem. 89, 52 (1985).
23. 10. Nichols, H. Taylor, P. Schmidt. J. Simons, J. Chem. Phys. 92, 340 (1990).
24. 18. Fletcher, Practical Methods of Optimization, Second Edition (Wiley, New York, 1987).
25. E.D. Glendening, J.K. Badenhoop, A.E. Reed, J.E. Carpenter, J.A. Bohmann, C.M. Morales, F. Weinhold, NBO 5.G. http://www.chem.wisc.edu/~nbo5.
26. Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/
27. 7. Schaftenaar, Molden3.2, CAOS/CAMM Center, University of Nijmegen (1997).
28. 19. Portmann, P.F. Fluekiger, CSCS/ETHZ and CSCS/UNI Geneva (2002).